2.1. 자연어 처리란
자연어(natural language) : 한국어, 영어 등 평소에 쓰는 말
자연어처리(Natural Language Processing, NLP) : 자연어를 처리하는 분야, 즉 사람의 언어를 컴퓨터에게 이해시키기 위한 기술
사람의 언어는 '문자'로 구성되며, 언어의 의미는 '단어'로 구성된다.
즉 단어는 의미의 최소 단위, 따라서 자연어를 컴퓨터에게 이해시키는 데는 '단어의 의미'를 이해시키는 것이 중요하다.
2.2. 시소러스
시소러스 : 유의어 사전으로 뜻이 같은 단어(동의어)나 뜻이 비슷한 단어(유의어)가 한 그룹으로 분류되어 있다.
ex) WordNet : 시소러스 중 하나

단어 사이의 '상위와 하위' 혹은 '전체와 부분' 등 더 세세한 관계까지 정의해둔 경우도 있다.

이처럼 모든 단어에 대한 유의어 집합을 만든 다음, 단어들의 관계를 그래프로 표현하여 단어 사이의 연결을 정의할 수 있다. 이 '단어 네트워크'를 이용해 컴퓨터에게 단어 사이의 관계를 가르칠 수 있고, 컴퓨터에게 단어의 의미를 이해시켰다고 주장할 수 있다.
✔️ 시소러스의 문제점
사람이 수작업으로 레이블링하는 방식에는 결점이 존재한다.
- 시대 변화에 대응하기 어렵다. : 시대에 따라 언어의 의미가 변하기도 하는데, 이를 대응하기 위해 사람이 수작업으로 끊임없이 갱신해야 한다.
- 사람을 쓰는 비용은 크다.
- 단어의 미묘한 차이를 표현할 수 없다. : ex) 빈티지 vs 레트로
이러한 문제점을 해결하기 위해 '통계 기반 기법', '추론 기반 기법'이 등장했다.
2.3. 통계 기반 기법
말뭉치(corpus) : 대량의 텍스트 데이터,
맹목적으로 수집된 텍스트 데이터가 아닌 자연어 처리 연구나 애플리케이션을 위해 수집된 테스트 데이터
✔️ 파이썬으로 말뭉치 전처리하기
말뭉치에 전처리(preprocessing)을 해보자.
여기서 전처리란 텍스트 데이터를 단어로 분할하고 그 분할된 단어들을 단어 ID 목록으로 변환하는 일이다.
def preprocess(text):
text = text.lower()
text = text.replace('.', ' .')
words = text.split(' ')
word_to_id = {}
id_to_word = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
corpus = np.array([word_to_id[w] for w in words])
return corpus, word_ti_id, id_to_wordtext = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
# (array([0, 1, 2, 3, 4, 1, 5, 6]),
# {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6},
# {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'})
✔️ 단어의 분산 표현
세상의 색들은 '코발트블루', '싱크레드'같은 고유한 이름을 붙일 수도 있지만 RGB라는 세가지 성분이 어떤 비율로 섞여 있느냐로 표현할 수도 있다. 전자는 색의 가짓수만큼 이름을 부여하고, 후자는 색을 3차원의 벡터로 표현한다.
RGB같은 벡터표현의 장점은 여러가지가 있는데,
1. 색을 더 정확하게 명시할 수 있다.
2. 모든 색을 3개의 성분으로 간결하게 표현할 수 있다.
3. 어떤 색인지 짐작하기 쉽다.
4. 색끼리의 관련성(비슷한 색인지 여부 등)이나 정량화하기도 쉽다.
색의 RGB처럼 단어도 벡터로 표현할 수 있을까?
분산표현(distributed representation) : '단어의 의미'를 정확하게 파악할 수 있는 벡터표현
✔️ 분포 가설
단어를 벡터로 표현할 때는 분포 가설(distributional hypothesis)인 '단어의 의미는 주변 단어에 의해 형성된다.'를 기초로 한다.
분포 가설이 의미하는 바는 단어 자체에는 의미가 없고 그 단어가 사용된 '맥락(context)'이 의미를 형성한다는 것이다.
ex) I drink beer, We drink wine -> drink 주변에는 음료가 등장하기 쉽다.
I guzzle beer, We guzzle wine -> guzzle(폭음하다)는 drink와 같은 맥락에서 사용되어 가까운 의미의 단어이다.
맥락 : 주목하는 단어 주변에 놓인 단어

이런 분포 가설에 기초해 단어를 벡터로 나타내는 방법을 생각해보자.
통계 기반(statistical based) 기법 : 어떤 단어에 주목했을 때 그 주변에 어떤 단어가 몇 번 등장하는지를 세어 집계하는 방법
✔️ 동시발생 행렬
그림 2-7의 각 행은 해당 단어를 표현한 벡터가 된다.
이 표가 행렬의 형태를 띤다는 뜻에서 동시발생 행렬(co-occurence matrix)라고 한다.
이처럼 동시발생 행렬을 활용하면 단어를 벡터로 나타낼 수 있다.

✔️ 벡터 간 유사도
벡터 사이의 유사도를 측정하는 방법은 벡터의 내적, 유클리드 거리 등으로 다양하다.
하지만 단어 벡터의 유사도를 나타낼 때는 코사인 유사도를 자주 이용한다.
코사인 유사도는 두 벡터가 가리키는 방향이 얼마나 비슷한가이다.
두 벡터의 바향이 완전히 같다면 1이 되고, 완전히 반대라면 -1이 된다.
분자는 벡터의 내적, 분모에는 각 벡터의 크기(벡터의 각 원소를 제곱해 더한 후 다시 제곱근을 구해 계산)으로,
핵심은 벡터를 정규화하고 내적을 구하는 것이다.
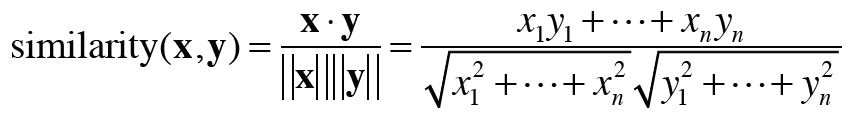
def cos_similarity(x, y, eps=1e-8):
# epsilon 값을 추가해,
# 0으로 나누기 오류가 나는 것을 막아줌
nx = x / np.sqrt(np.sum(x**2) + eps) # x의 정규화
ny = y / np.sqrt(np.sum(y**2) + eps) # y의 정규화
return np.dot(nx, ny)
이를 활용하여 You와 i의 코사인 유사도를 구하면 약 0.7로 -1와 1사이의 값이므로 비교적 높다고 할 수 있다.
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
c0 = C[word_to_id['you']] # "you"의 단어 벡터
c1 = C[word_to_id['i']] # 'i'의 단어 벡터
print(cos_similarity(c0, c1))
# 0.7071067691154799
2.4. 통계 기반 기법 개선하기
✔️ 상호 정보량
앞 절에서 동시발생 행렬의 원소는 두 단어가 동시에 발생한 횟수를 나타낸다.
하지만 이 발생횟수라는 것이 좋은 특징이 아닌데, 말뭉치에서 'the'와 'car'의 동시발생을 생각해보자.
'... the car ...' 이라는 문구가 자주 보일텐데 'car'는 'drive'와 관련성이 훨씬 깊다.
하지만 'the'가 고빈도 단어라서 'car'와 강한 관련성을 갖는다고 평가가 될 것이다.
이러한 문제를 해결하기 위해 점별 상호정보량(Pointwise Mutual Information, PMI)라는 척도를 사용한다.

P(x)는 x가 일어날 확률, P(y)는 y가 일어날 확률, P(x, y)는 x, y가 동시에 일어날 확률로, PMI가 높을수록 관련성이 높다.
식 2-2를 동시발생 행렬을 사용하여 식 2-3으로 만들 수 있다.
C는 동시발생 행렬, C(x, y)는 단어 x, y가 동시발생하는 횟수, C(x), C(y)는 각각 단어 x, y의 등장횟수, N은 말뭉치에 포함된 단어 수
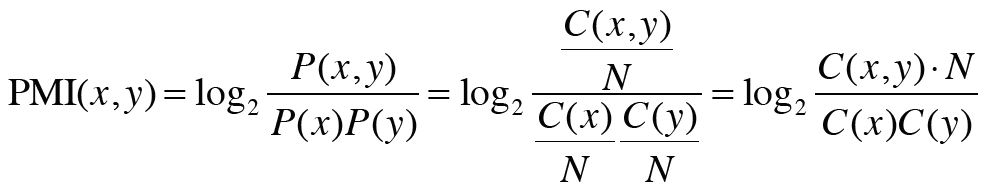
예를 들어 말뭉치 단어의 수(N)은 10000이며, 'the'는 1000번, 'car'는 20번, 'drive'는 10번 발생했다고 해보자.
이 때, 동시발생 횟수 관점에서는 'car'는 'drive'보다 'the'와 관련이 깊다.
하지만 PMI 관점에서는 식 2-5처럼 'dirve'와 관련성이 강해진다.


하지만 PMI도 한가지 단점이 있는데 동시발생 횟수가 0이면 log2 0으로 -inf가 된다는 것이다.
이를 피하기 위해 실제로 구현할 때는 양의 상호정보량(Positive PMI, PPMI)를 사용한다.
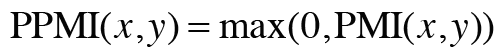
def ppmi(C, verbose=False, eps=1e-8):
'''PPMI(점별 상호정보량) 생성
:param C: 동시발생 행렬
:param verbose: 진행 상황을 출력할지 여부
:return: ppmi
'''
M = np.zeros_like(C, dtype=np.float32)
N = np.sum(C) # num of corpus
S = np.sum(C, axis=0) # 각 단어의 출현 횟수
total = C.shape[0] * C.shape[1]
cnt = 0
for i in range(C.shape[0]):
for j in range(C.shape[1]):
pmi = np.log2(C[i, j] * N / (S[i]*S[j]) + eps)
M[i, j] = max(0, pmi)
if verbose:
cnt += 1
if cnt % (total//100) == 0:
print(f'{(100*cnt/total):.2f} 완료')
return M
PPMI를 활용하여 동시발생 행렬을 PPMI 행렬로 전환할 수 있다.

이로써 PPMI행렬이라는 좋은 척도를 얻었지만 PPMI행렬에도 여전히 큰 문제가 있다.
말뭉치의 어휘수가 증가함에 따라 각 단어 벡터의 차원수도 증가한다는 것이다.
예를 들어 말뭉치의 어휘수가 10만개라면 그 벡터의 차원수도 똑같이 10만이 된다.
또한, 대부분의 원소가 0인 것을 볼 수 있는데, 이는 각 원소의 중요도가 낮다는 것을 뜻한다.
이러한 벡터는 노이즈에 약하고 견고하지 못하다. 이를 대처하기 위한 방법이 벡터의 차원 감소이다.
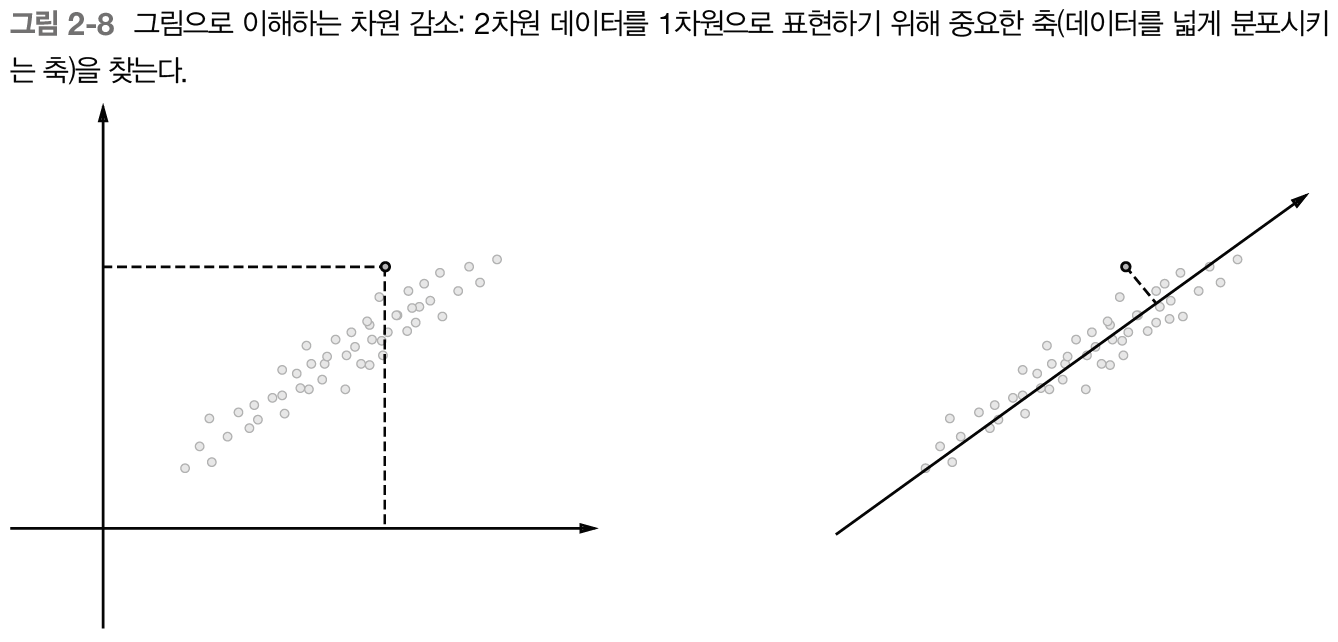
✔️ 차원 감소
차원감소(dimensionality reduction) : 중요한 정보는 최대한 유지하면서 벡터의 차원을 줄이는 방법
그림 2-8의 왼쪽은 2차원 좌표에 데이터점들을 표시, 오른쪽은 새로운 축을 도입해 똑같이 데이터를 좌표축 하나만으로 표시했다.
이 때 각 데이터값은 새로운 축으로 사영된 값으로 변한다.
여기서 1차원값만으로도 데이터의 본질적인 차이를 구별할 수 있어야 하며, 다차원 데이터에도 적용할 수 있다.
특잇값분해(Singular Value Decomposition, SVD) : 임의의 행렬을 세 행렬의 곱으로 분해

U, V는 직교행렬, S는 대각행렬
U는 단어 공간, S의 대각성분에는 특잇값(singular value)이 큰 순서로 나열되어 있는데, 여기서 특잇값이란 해당 축의 중요도로 간주할 수 있다.

여기서 그림 2-10과 같이 중요도가 낮은 원소(특잇값이 작은 원소)를 깎아낸다.
S의 특잇값이 작다면 중요도가 낮다는 뜻이므로, U에서 여분의 열벡터를 깎아내어 원래의 행렬을 근사할 수 있다.

이처럼 SVD를 적용한 그래프는 그림 2-11과 같다.

goodbye와 hello, you와 i가 제법 가까이 있음을 알 수 있다.
2.5. 정리
- WordNet 등의 시소러스를 이용하면 유의어를 얻거나 단어 사이의 유사도를 측정하는 등 유용한 작업을 할 수 있다.
- 시소러스 기반 기법은 시소러스를 작성하는 데 엄청난 인적 자원이 든다거나 새로운 단어에 대응하기 어렵다는 문제가 있다.
- 현재는 말뭉치를 이용해 단어를 벡터화하는 방식이 주로 쓰인다.
- 최근의 단어 벡터화 기법들은 대부분 '단어의 의미는 주변 단어에 의해 형성된다'는 분포 가설에 기초한다.
- 통계 기반 기법은 말뭉치 안의 각 단어에 대해 그 단어의 주변 단어의 빈도를 집계한다.(동시발생 행렬)
- 동시발생 행렬을 PPMI 행렬로 변환하고 다시 차원을 감소시킴으로써, 거대한 '희소벡터'를 작은 '밀집벡터'로 변환할 수 있다.
- 단어의 벡터공간에서는 의미가 가까운 단어는 그 거리도 가까울 것으로 기대된다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥부터시작하는딥러닝2] Chapter 4. word2vec 속도 개선 (0) | 2024.04.19 |
|---|---|
| [밑바닥부터시작하는딥러닝2] Chapter 3. word2vec (0) | 2024.04.18 |
| [밑바닥부터시작하는딥러닝1] Chapter 8. 딥러닝 (0) | 2024.04.16 |
| [밑바닥부터시작하는딥러닝1] Chapter 7. 합성곱 신경망(CNN) (0) | 2024.04.13 |
| [밑바닥부터시작하는딥러닝1] Chapter 6. 학습관련기술들 (1) | 2024.04.12 |