8.1. 더 깊게
정확도를 개선하기 위해서 앙상블학습, 학습률 감소, 데이터 확장 등을 사용할 수 있다.
데이터 확장(data argumentation)은 입력 이미지(훈련 이미지)를 알고리즘을 동원해 인위적으로 확장한다.
그림 8-4와 같이 입력 이미지를 회전하거나 세로로 이동하는 등 미세한 변화를 주어 이미지의 개수를 늘리는 것이다.
이는 특히 데이터가 많이 없을 때 효과적인 수단이다.

데이터 확장은 이미지 일부를 잘라내는 crop, 좌우를 뒤집는 flip등의 방법이 있다.
✔️ 층을 깊게 하는 이유
층을 깊게 하면 신경망의 매개변수 수가 줄어든다.
합성곱 연산에서 필터의 크기에 주목해 생각해보면 쉽게 이해될 것이다.
그림 8-5는 5*5 필터로 구성된 합성곱 계층, 그림 8-6은 3*3 필터로 합성곱 연산을 2회 반복하는 경우이다.
5*5 합성곱 연산 1회는 3*3 합성곱 연산을 2회 수행하여 대체할 수 있다. 이 때 전자의 매개변수는 25개(5*5), 후자는 18개(2*3*3)이며, 매개변수 수는 층을 반복수록 적어진다.


또한 학습의 효율성이 좋아진다. 즉 학습 데이터의 양을 줄여 학습을 고속으로 수행할 수 있다.
앞단의 합성곱 계층에서는 엣지 등의 단순한 패턴에 뉴런이 반응하고 층이 깊어지면서 텍스처와 사물의 일부와 같이 점차 더 복잡한 것에 반응한다.
이것은 강아지를 인식하는 문제라면 얕은 신경망으로는 강아지의 특징 대부분을 한 번에 이해해야 한다는 뜻이다.
견종도 다양하고 어느 각도에서 찍은 사진이냐에 따라 완전히 다르게 보이기 때문에 특징을 이해하려면 변화가 풍부하고 많은 학습 데이터가 필요하며, 결론적으로 학습시간이 오래걸린다.
그러나 신경망을 깊게 하면 학습해야 할 문제를 계층적으로 분해할 수 있다.
8.2. 딥러닝의 초기 역사
✔️ VGG
합성곱 계층과 풀링 계층으로 구분되는 기본적인 CNN
비중있는 층(합성곱 계층, 완전연결 계층)을 모두 16층(or 19층)으로 심화했다.
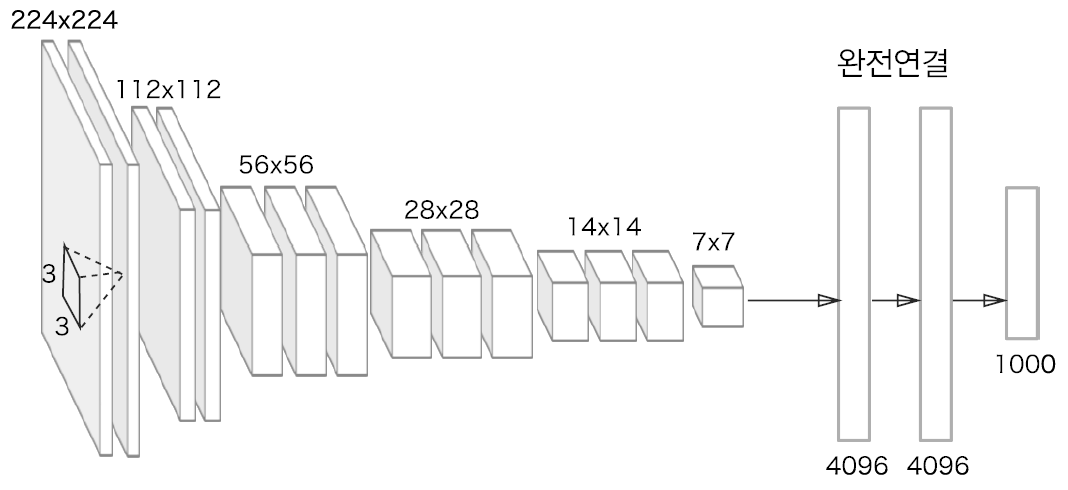
3*3의 작은 필터를 사용한 합성곱 계층을 연속으로 거친다.
그 과정에서 연속으로 풀링 계층을 두어 크기를 절반으로 줄이는 작업을 반복한다.
그 후 마지막에는 완전연결 계층을 통과시켜 결과를 출력한다.
✔️ GoogLeNet
그림 8-10의 사각형이 합성곱 계층과 풀링 계층 등의 계층을 나타낸다.
구성이 복잡해보이지만 기본적인 CNN과 다르지 않다. 단, 세로방향 뿐만 아니라 가로방향도 깊다는 것이 특징이다.

GoogLeNet은 가로방향에 '폭'이 있는데 이를 인셉션 구조라 한다.
크기가 다른 필터와 풀링을 여러개 적용하여 그 결과를 결합한다.
이 인셉션 구조를 하나의 빌딩 블록(구성요소)으로 사용하는 것이 GoogLeNet의 특징이다.
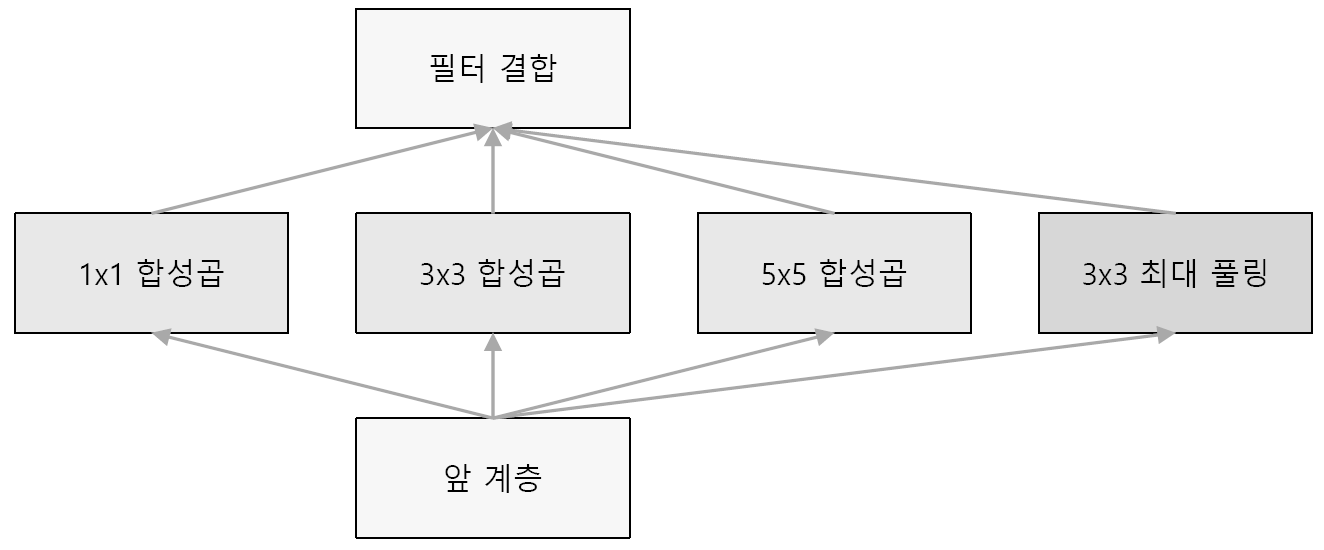
또한, 1*1크기의 필터를 사용한 합성곱계층을 많은 곳에서 사용한다.
1*1의 합성곱 연산은 채널 쪽으로 크기를 줄이는 것으로 매개변수 제거와 고속처리에 기여한다.
✔️ ResNet
딥러닝의 학습에서는 층이 지나치게 깊으면 학습이 잘 되지 않고 오히려 성능이 떨어지는 경우도 많다.
이를 해결하기 위해 스킵 연결(skip connection)을 도입한다.
스킵연결 : 입력 데이터를 합성곱 계층을 건너뛰어 출력에 바로 더하는 구조
입력데이터를 그대로 흘리는 것으로 역전파 때도 상류의 기울기를 그대로 하류로 보낸다.
그래서 스킵연결로 기울기가 작아지거나 지나치게 커질 걱정없이 앞 층에 의미있는 기울기가 전해질 것을 기대할 수 있다.
층을 깊게 할수록 기울기가 작아지는 소실 문제를 줄여줄 수 있다.
그림 8-12에서는 입력 x를 연속한 두 합성곱 계층을 건너뛰어 출력에 바로 연결한다.
이 단축 경로가 없다면 두 합성곱 계층의 출력이 F(x)가 되지만 스킵연결로 인해 F(x) + x가 되었다.
스킵연결은 층이 깊어져도 학습을 효율적으로 할 수 있도록 도와주는데 이는 역전파 때 스킵연결이 신호 감쇠를 막아주기 때문이다.

ResNet은 VGG신경망을 기반으로 스킵연결을 도입하여 층을 깊게 하였다.
그림 8-13과 같이 합성곱계층을 2개 층마다 건너뛰면서 층을 깊게 한다.

8.6. 정리
- 수많은 문제에서 신경망을 더 깊게하여 성능을 개선할 수 있다.
- 유명한 신경망으로는 VGG, GoogLeNet, ResNet이 있다.
- GPU와 분산 학습, 비트 정밀도 감소 등으로 딥러닝을 고속화할 수 있다.
참고 git : https://github.com/geonsangyoo/DeepLearning/tree/master
'Deep Learning' 카테고리의 다른 글
| [밑바닥부터시작하는딥러닝2] Chapter 3. word2vec (0) | 2024.04.18 |
|---|---|
| [밑바닥부터시작하는딥러닝2] Chapter 2. 자연어와 단어의 분산 표현 (0) | 2024.04.17 |
| [밑바닥부터시작하는딥러닝1] Chapter 7. 합성곱 신경망(CNN) (0) | 2024.04.13 |
| [밑바닥부터시작하는딥러닝1] Chapter 6. 학습관련기술들 (1) | 2024.04.12 |
| [밑바닥부터시작하는딥러닝1] Chapter 5. 오차역전파법 (0) | 2024.04.05 |