6.1. RNN의 문제점
BPTT에서 기울기 소실 혹은 기울기 폭발이 일어나기 때문에 시계열 데이터의 장기 의존 관계를 학습하기 어렵다.
그림 6-5에서 시간방향 기울기에 주목하면 'tanh', '+', 'MatMul(행렬곱)' 연산을 통과하는 것을 알 수 있다.
여기서 +는 기울기를 그대로 하류로 흘려보내기 때문에 기울기가 변하지 않지만 나머지 두 연산은 기울기를 변화시킨다.

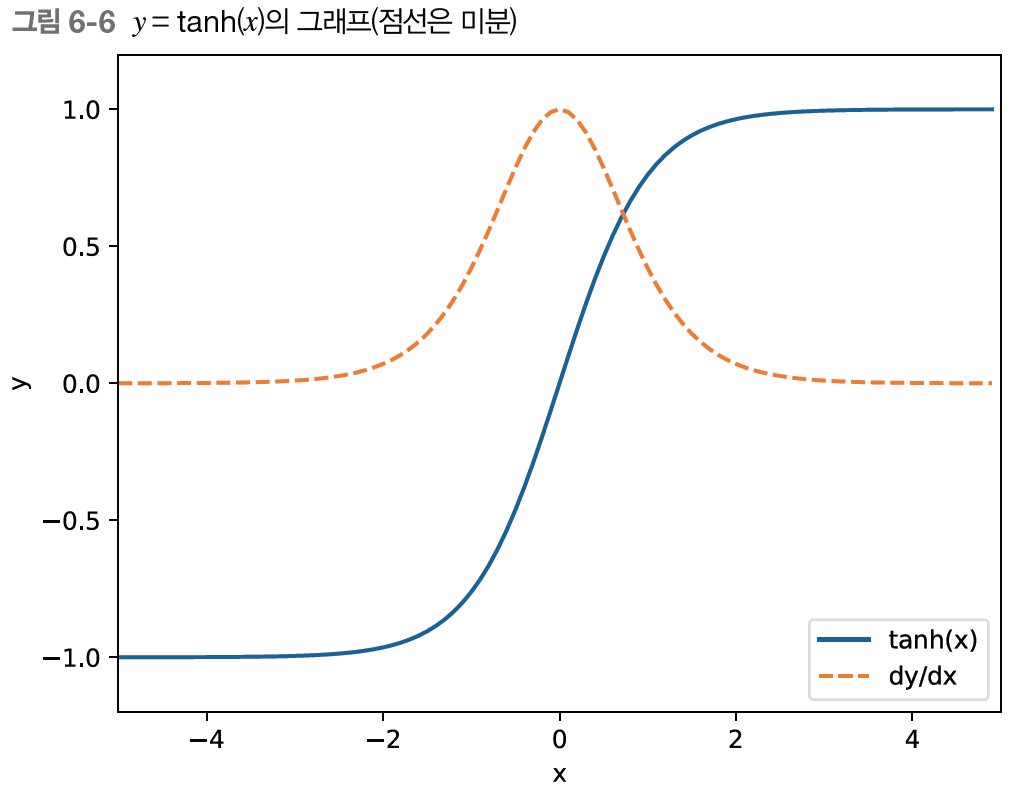
그림 6-6에서 tanh(x)의 미분인 점선을 보면 값이 1 이하이고 x가 0으로부터 멀어질수록 작아진다.
이는 역전파에서 기울기가 tanh노드를 지날 때마다 작아진다는 뜻이다.
MatMul(행렬곱)을 보면 그림 6-7처럼 상류로부터 dh라는 기울기가 계속 흘러온다고 가정하자.
이 때 MatMul 노드의 역전파는 dhWh^T라는 행렬곱으로 기울기를 계산하는데, 같은 계산을 시계열 데이터의 시간 크기만큼 반복한다.

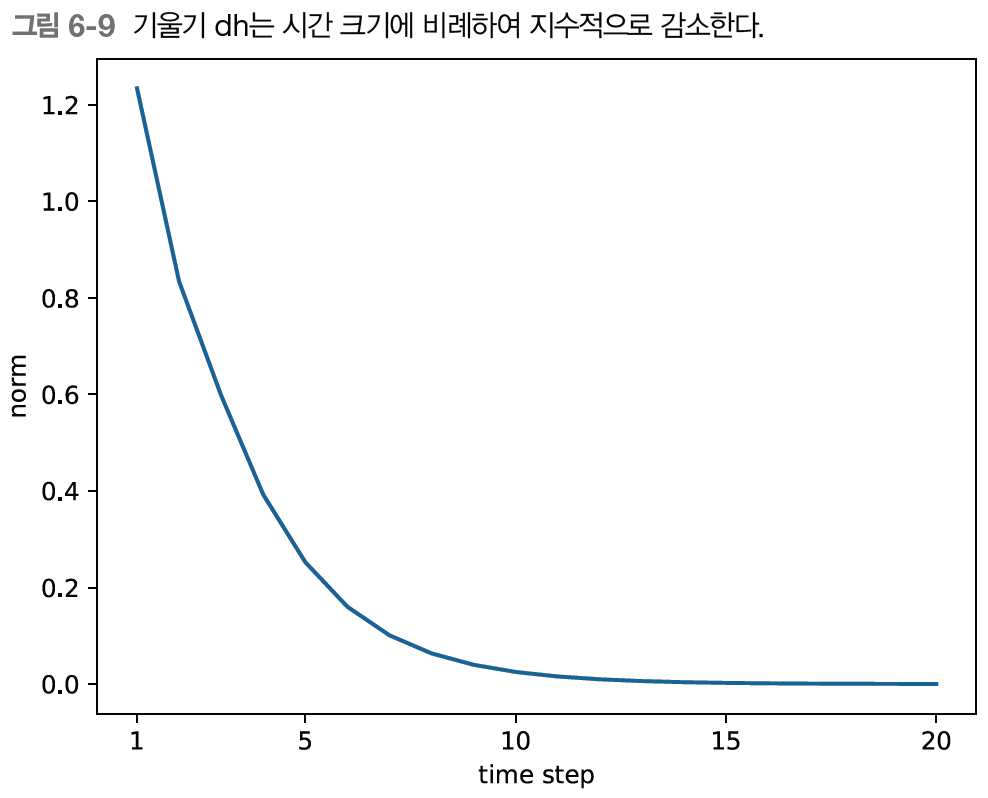
이렇게 Wh를 T번 반복하여 dh 기울기가 계속 흘러온다면, 그림 6-8의 기울기 폭발(exploding gradients)이나 그림 6-9의 기울기 소실(vanishing gradients)이 일어난다.

✔️ 기울기 폭발 대책
기울기 폭발의 대책으로는 기울기 클리핑(gradients clipping)이라는 기법이 있다.

모든 매개변수에 대한 기울기를 g로 처리한다고 가정하고 threshold를 문턱값으로 설정해보자.
이 때 기울기의 L2노름(||g||)이 문턱값을 초과하면 두번짜 줄의 수식과 같이 기울기를 수정한다.
6.2. 기울기 소실과 LSTM
기울기 소실의 문제를 해결하기 위해 RNN에서 게이트가 추가한 아키텍처(LSTM, GPU 등)가 제안되고 있다.

c(기억 셀 memory cell)이 추가된 것을 볼 수 있다.
기억 셀은 데이터를 자기 자신으로만(LSTM 계층 내에서만) 주고받는 특징이 있다.
즉, LSTM 계층 내에서만 완결되고 다른 계층으로는 출력하지 않는다.
반면, LSTM의 은닉 상태 h는 RNN계층과 마찬가지로 다른 계층으로(위쪽으로) 출력된다.
LSTM의 기억 셀 ct는 과거로부터 시각 t까지 필요한 모든 정보가 저장되어 있다고 가정한다.
그리고 필요한 정보를 모두 간직한 기억을 바탕으로 외부 계층에(+ 다음 시각의 LSTM에) 은닉 상태 ht를 출력한다.
이 때 출력하는 ht는 그림 6-12와 같이 기억 셀의 값을 tanh함수로 변환한 값이다.

그럼 여기서 '게이트'의 기능이 뭘까?
게이트는 데이터의 흐름을 제어한다.
그림 6-13처럼 물의 흐름을 멈추거나 배출하고, 그림 6-14처럼 어느 정도 열지를 조절한다.
이러한 열지말지, 얼마나 열지를 데이터로부터 학습한다.


✔️ output 게이트
그럼 tanh(ct)에 게이트를 적용한다면, yanh(ct)의 각 원소에 대해 '그것이 다음 시각의 은닉 상태에 얼마나 중요한가'를 조정한다.
이 게이트는 다음 은닉 상태 ht의 출력을 담당하는 게이트이므로 output 게이트(출력 게이트)라고 한다.
output 게이트의 열림 상태는 입력 xt와 이전 상태 ht-1로부터 구한다.
(가중치 매개변수와 편향에 output의 첫글자이 o를 첨자로 추가, 시그모이드 함수는 σ)


이 때 ht는 식 6-2와 같이 o와 tanh(ct)의 곱으로 계산되는데 여기서 '곱'은 원소별 곱으로 아다마르 곱(Hadamard product)라고도 한다.

✔️ forget 게이트
이제 기억 셀 갱신 부분을 살펴보면 우리는 기억 셀에 '무엇을 잊을까'를 명확하게 지시해야 한다.
이처럼 ct-1의 기억 중에 불필요한 기억을 잊게 해주는 게이트를 forget 게이트(망각 게이트)라 부른다.


ct는 forget 게이트의 출력 f와 이전 기억 셀인 ct-1의 원소별 곱, ct=f⊙ct−1 로 계산한다.
✔️ 새로운 기억 셀
forget 게이트를 통해 이전 시각의 기억 셀로부터 잊어야 할 기억을 삭제했다.
그럼 새로 기억해야 할 정보를 기억 셀에 추가해보자.
그림 6-17처럼 tanh 노드가 계산한 결과를 이전 시각의 기억 셀 ct-1에 더한다.
여기서 tanh 노드는 '게이트'가 아니며, 새로운 '정보'를 기억 셀에 추가하는 것이 목적이다.
따라서 활성화 함수로 시그모이드 함수가 아닌 tanh 함수를 사용한다.

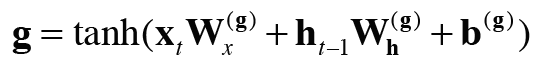
✔️ input 게이트
g에 input 게이트(입력 게이트)를 추가한다.
input 게이트는 g의 각 원소가 새로 추가되는 정보로써의 가치가 얼마나 큰지를 판단한다.


이 후 i와 g의 원소별 곱 결과를 기억 셀에 추가한다.
✔️ LSTM의 기울기 흐름
LSTM은 어떤 원리로 기울기 소실을 없애주는 걸까?
그림 6-19에서 기억 셀에만 집중하여 역전파의 흐름을 살펴보자.

기억셀의 역전파는 '+'와 'x'노드만 지니게 되는데, '+'노드는 상류에서 전해지는 기울기를 그대로 흘려 기울기 변화(감소)는 일어나지 않는다.
'x'노드는 '행렬 곱'이 아닌 '원소별 곱(아마다르 곱)'이 이뤄지며, 매 시각 다른 게이트 값을 이용해 원소별 곱을 계산하므로 곱셈의 효과가 누적되지 않아 기울기 소실이 일어나지 않는다.
이 'x'노드는 forget 게이트가 제어하는데, '잊어야 한다'고 판단한 기억 셀의 원소에 대해서는 기울기가 작아지고 '잊어서는 안된다'고 판단한 원소에 대해서는 기울기가 약화되지 않은 채 과거방향으로 전해져 기울기 소실없이 전파되리라 기대한다.
6.3. LSTM 구현
LSTM에서 수행하는 계산은 아래와 같다.

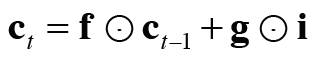

식 6-6의 네 수식에 포함된 아핀 변환(xW + hW + b 형태의 식)을 하나의 식으로 정리해 계산한다.

하나의 식으로 정리된 Wx, Wh, b를 활용하여 그림 6-21과 같이 계산할 수 있다.
4개 분의 아핀 변환을 한꺼번에 수행한 후 slice노드를 통해 아핀 변환의 결과를 균등하게 네조각으로 나눠 전달한다.

LSTM의 구체적인 구현과 LSTM을 이용한 언어모델 구현은 https://github.com/ExcelsiorCJH/DLFromScratch2.git 참고
참고로 Time LSTM와 Time RNN을 구현하는 것은 흡사하며, RNN을 활용한 언어모델과 LSTM을 활용한 언어모델도 흡사하다.
6.5. RNNLM 추가 개선
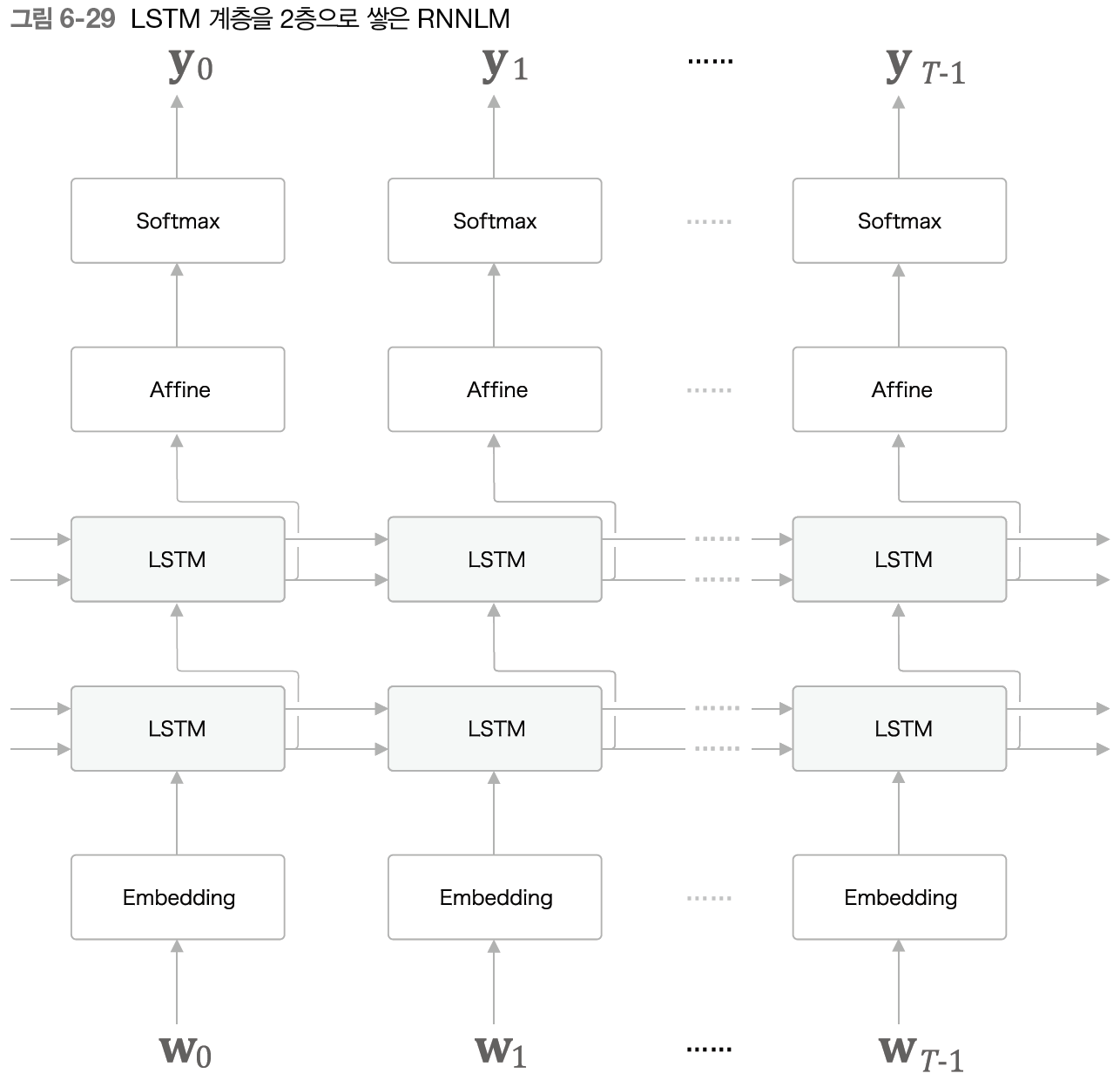
✔️ LSTM 계층 다층화
RNNLM으로 정확한 모델을 만들고자 한다면 LSTM 계층을 깊게 쌓아 효과를 볼 수 있다.
첫번째 LSTM 계층의 은닉 상태가 두번째 LSTM 계층에 입력되고 이것이 반복된다.
그 결과 더 복잡한 패턴을 학습할 수 있게 된다.
✔️ 드롭아웃에 의한 과적합 억제
LSTM 계층을 다층화하면 시계열 데이터의 복잡한 의존 관계를 학습할 수 있다.
하지만 이런 모델은 종종 과적합(overfitting)을 일으킨다.
이를 억제하기 위해 '훈련 데이터의 양 늘리기', '모델의 복잡도 줄이기', 모델의 복잡도에 페널티를 주는 '정규화(normalization)' 등이 있다.
드롭아웃(dropout)처럼 훈련 시 계층 내의 뉴런 몇 개를 무작위로 무시하고 학습하는 방법도 일종의 정규화라고 볼 수 있다.

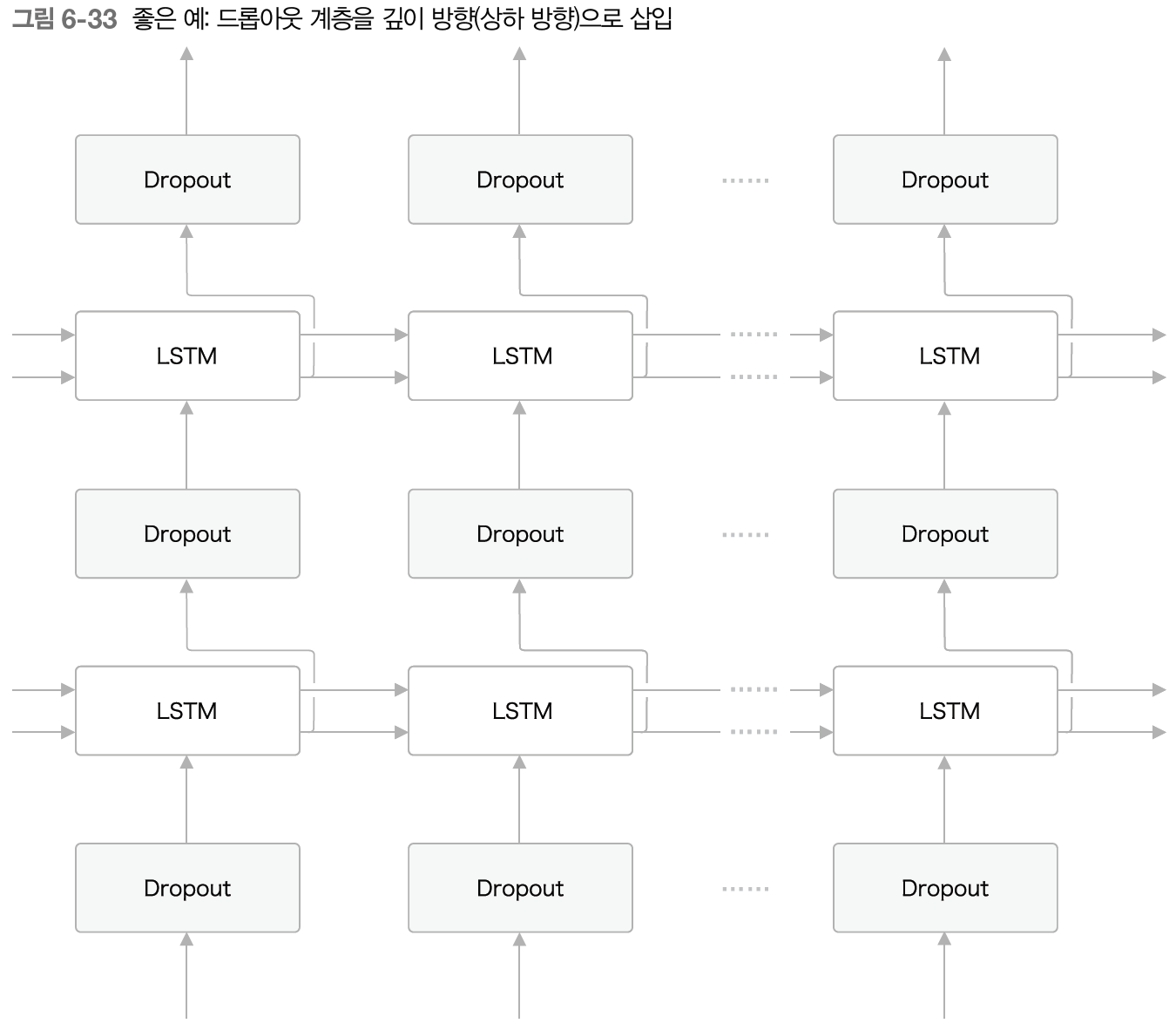
그림 6-32처럼 시계열방향으로 드롭아웃을 넣는다면 시간이 흐름에 따라 정보가 사라질 수 있다. 즉 흐르는 시간에 비례해 드롭아웃에 의하 노이즈가 축적된다.

따라서 그림 6-33과 같이 시계열방향이 아닌 깊이방향(상하 방향)으로 삽입하는 것이 좋다.
✔️ 가중치 공유(weight tying)
그림 6-35처럼 두 계층이 가중치를 공유함으로써 학습하는 매개변수 수가 줄어드는 동시에 정확도도 향상된다.

✔️ 개선된 RNNLM 구현
개선된 RNNLM은 그림 6-36과 같고 구체적인 구현은 https://github.com/ExcelsiorCJH/DLFromScratch2.git 참고

6.6. 정리
- 단순한 RNN의 학습에서는 기울기 소실과 기울기 폭발이 문제가 된다.
- 기울기 폭발에는 기울기 클리핑, 기울기 소실에는 게이트가 추가된 RNN(LSTM과 GRU 등)이 효과적이다.
- LSTM에는 input게이트, forget 게이트, output 게이트 등 3개의 게이트가 있다.
- 게이트에는 전용 가중치가 있으며, 시그모이드 함수를 사용해 0.0~1.0 사이의 실수를 출력한다.
- 언어 모델 개선에는 LSTM 계층 다층화, 드롭아웃, 가중치 공유 등의 기법이 효과적이다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥부터시작하는딥러닝2] Chapter 8. 어텐션 (0) | 2024.04.23 |
|---|---|
| [밑바닥부터시작하는딥러닝2] Chapter 7. RNN을 사용한 문장 생성 (0) | 2024.04.22 |
| [밑바닥부터시작하는딥러닝2] Chapter 5. 순환 신경망(RNN) (0) | 2024.04.20 |
| [밑바닥부터시작하는딥러닝2] Chapter 4. word2vec 속도 개선 (0) | 2024.04.19 |
| [밑바닥부터시작하는딥러닝2] Chapter 3. word2vec (0) | 2024.04.18 |