L1 Norm, L2 Norm / L1 Loss, L2 Loss 이란?

📌 Norm

벡터의 크기를 측정하는 방법

두 벡터 사이의 거리를 측정하는 방법

 

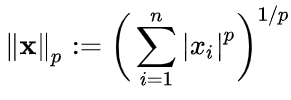
📌 L1 Norm

Norm 식에서 p가 1인 Norm으로 벡터의 요소에 대한 절댓값의 합

Manhattan(맨허튼) norm이라고도 한다.

L2보다 outlier(이상치)에 robust(덜 민감)하다.

 

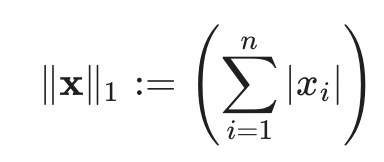
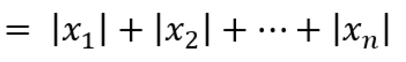
📌 L2 Norm

Norm 식에서 p가 2인 Norm으로 피타고라스 정리를 활용했다.

Euclidean(유클리드) norm이라고도 한다.

제곱의 형태이기 때문에 outlier(이상치)에 예민하나 더욱 일반화된 모델을 생성한다.

 

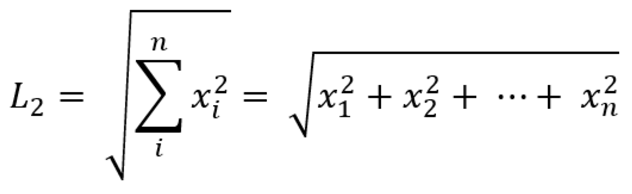
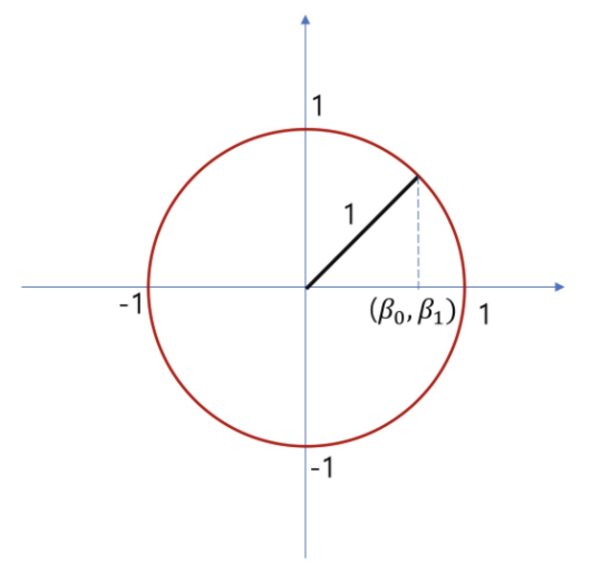
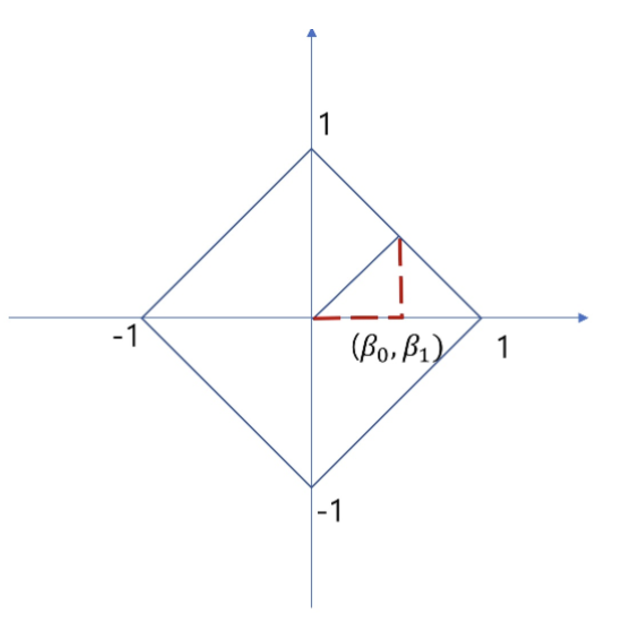
📌 L1 Norm, L2 Norm 비교

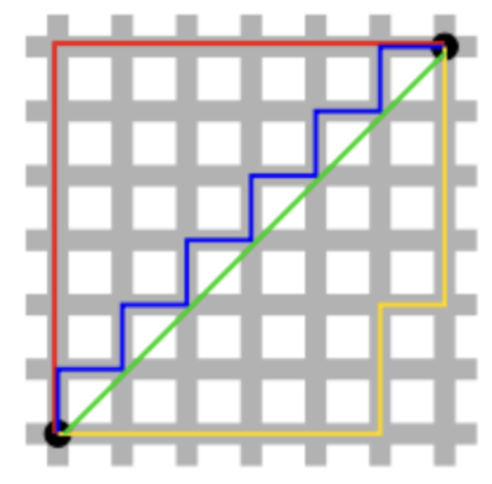
L1은 초록색 외의 선들로 여러가지 path를 가지지만

L2는 초록색 선으로 unique shortest path를 가진다.

 

 

Loss도 Norm과 유사하게 계산된다.

📌 L1 Loss

MAE(Mean Absolute Error)로, 실제값과 예측값 오차의 절댓값 합

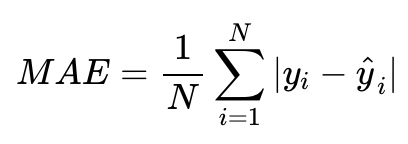
따라서 L1 Loss가 L2 Loss보다 outlier(이상치)에 좀 더 robust(덜 민감)하다.

 

 

📌 L2 Loss

MSE(Mean Squared Error)로, 실제값과 예측값 오차의 제곱의 합

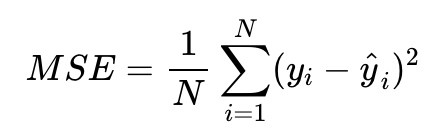
L1 Loss와 반대로 상황에 따라 outlier가 중요하다면 L2 Loss를 사용하는 것이 좋다.

 

 

참고 :

https://hwanii-with.tistory.com/58

https://based-infos.tistory.com/10

https://thflgg133.tistory.com/231